Dziś Światowy Dzień Statystyki, czyli niby radość, ale nie ma co udawać, wszyscy wiemy, że gdyby nasza jubilatka zechciała zorganizować z tej okazji przyjęcie, to to by nie była najbardziej udana prywatka na świecie i najbardziej liczna też nie. To znaczy – może od biedy jakiś iloraz by przyszedł, ale weźcie sobie wyobraźcie tę niezręczność, że statystyka cała podjarana otwiera drzwi, patrzy, a tam iloraz, na co ona pyta: „a gdzie reszta?”. No i tak by siedzieli smutno we dwójkę, świętując dużymi kawałkami wykresu tortowego, ha ha, czaicie TORTOWEGO.

Bo widzicie, to nawet nie chodzi o to, że statystyka nie jest lubiana w tej szkole dyscyplin naukowych, ona jest wręcz szykanowana. Wszyscy rzucają w nią kulkami z papieru, kradną kalosze z szatni, a potem jeszcze ośmieszają za pomocą trójnogich psów, co to trzymają głowę w piekarniku, a ogon w lodówce i wtedy jest im w sam raz. Tymczasem dzisiaj, z okazji tak pięknego święta, chciałabym byśmy zastanowili się nad tym zagadnieniem na styku filozofii nauki i warzyw kapustnych. A mianowicie: czy istnieją głąby matematyczne? 

Może gdyby nauka statystyki polegała na obcowaniu z kruchymi ciasteczkami w kształcie rozkładu Gaussa, to królowa nauk miałaby lepszy PR?

I to nie jest tak, że ja to pytanie sobie wymyśliłam, stojąc w kolejce w warzywniaku, że tak sobie patrzyłam na te główki kapusty okrągłe, co to opisać je można wzorem (x-x_0)^2+(y-y_0)^2+(z-z_0)^2\leqslant R^2 (w formacie TeX-a) i wtedy naszła mnie myśl taka gwałtowna, że o co chodzi z tą polityką nienawiści względem warzyw kapustnych i królowej nauk. Wielu badaczy mnie wyprzedziło, co mnie w ogóle nie dziwi, jestem przyzwyczajona do takiego stanu rzeczy już od podstawówki, kiedy to mieliśmy biegać dookoła boiska na czas. 

Uwaga, oto jest nasza dzisiejsza Beata Kozidrak (w sensie, że gwiazda) matematyki – number sense, czyli nasze intelektualne możliwości do liczenia i szacowania. Rzadko kiedy jest w świetle reflektorów, „Gwiazdy tańczą na lodzie” by raczej nie wygrał, niemniej hej, nie uważacie, że to super ciekawe, czy te nasze zdolności do zarządzania cyferkami są kwestią genetyki czy też raczej edukacji i wychowania? No to sprawdźmy. A zacznijmy to śledztwo od kluczowego pytania: czy warto zabrać mątwę na maturę z matematyki?

Odpowiadam: a i owszem, świetnie się sprawdzi zamiast liczydła. Zdecydowanie warto następnym razem spakować tego miłego głowonoga wraz z ołówkiem i cyrklem, albowiem gdy takiej mątwie przedstawi się grupę dwóch krewetek i trzech krewetek, to one nie dadzą się oszukać, podpłyną tam, gdzie czeka na nich większa porcja obiadu. Nawet gdy krewetki były zbite w jedną kulkę niczym bajaderka! Brawo mątwy! Kto wie, może jak te miłe zwierzątka jeszcze poćwiczą to dogonią swoje koleżanki mrówki, które umieją liczyć aż do dwudziestu. Tak jest, jak takie mrówki sobie maszerują do kopca, to przy odliczaniu totalnie się zorientują, że gdzieś im się Stefan zgubił, pewnie znowu wszedł w żywicę i trzeba go rozkuwać. W poszukiwaniach zaś chętnie pomogą im szympansy, które gdy mają do wyboru pudełka z mniejszą lub większą liczbą skrawków czekolady, to bez wahania wybiorą to, gdzie czekolady będzie najwięcej, co dla mnie jest ostatecznym dowodem na to, że jednak pochodzę od małpy. 

Oprócz wyżej wymienionych zwierzątek o pomoc przy rozwiązywaniu sudoku warto poprosić niedźwiedzia, kruka, gołębia, a także muszkę owocówkę. A przy okazji, jak już nam będą w tych zagadkach pomagać, to warto pochwalić je, że ich przypadki nauczyły nas, że neurologiczne mechanizmy odpowiadające za podstawowe umiejętności arytmetyczne zostały wyodrębnione setki milionów lat temu (coooooooo?).

Nie możemy więc wykluczyć, że jakby tak dinozaurom dać do policzenia jakieś pola figur płaskich, to ani by im była w głowie ucieczka z Jurassic parku. 

Naprawdę mam w sobie przekonanie graniczące z pewnością, że ze statystyką każdemu do twarzy!

A teraz czas na dzieci! Ileż to było badań na niemowlakach! Oczywiście jak możecie się spodziewać badanie zmysłu matematycznego u dzieci było trochę bardziej skomplikowane niż nakazanie im rozwiązywać zadania z „I ty zostaniesz Pitagorasem”. W przypadku dzieci, które jeszcze nie umiały mówić najczęściej w eksperymentach pokazywano niemowlakom różną liczbę identycznych zabawek, pozwalając im wybrać do której grupy sobie podpełzną, lub zza specjalnej kurtyny wykonywano poprawne i niepoprawne działania matematyczne. Na przykład na oczach danego mikroczłowieka dodawano dwie lalki do jednej, a chwilę później jedna lalka znikała, sprawiając, że wynikiem dodawania 2+1 było 2. Następnie mierzono ile czasu dany niemowlak patrzy na wynik działania. O ile w przypadku poprawnych wyników dzieci nie spędzały zbyt dużo czasu na analizowaniu sytuacji, o tyle w przypadku niepoprawnych wyników dodawania czy odejmowania wpatrywały się w zabawki znacznie dłużej, najpewniej zastanawiając się WTF. 

Dużo było takich badań (znajdziecie je w bibliografii na końcu tego wpisu), w których sprawdzano umiejętność szacowania u dzieci półrocznych, trzyletnich, sześcioletnich i nastolatkach.

Ich wyniki wskazują na to, że kompetencje numeryczne są niezależne od języka i obecne od urodzenia.

A byli i badacze, którzy kochali kapustę tak bardzo, że postanowili bronić jej honoru jeszcze bardziej – Maria Tosto i jej naukowa drużyna trzasnęli w 2014 roku ogromne badanie z udziałem szesnastoletnich bliźniąt. Niestety, mnie i mojego brata bliźniaka do tego badania nie zaprosił, nad czym boleje bardzo, zwłaszcza jeśli miałoby się okazać, że to badanie również obejmowało porównywanie różnych ilości czekolady.

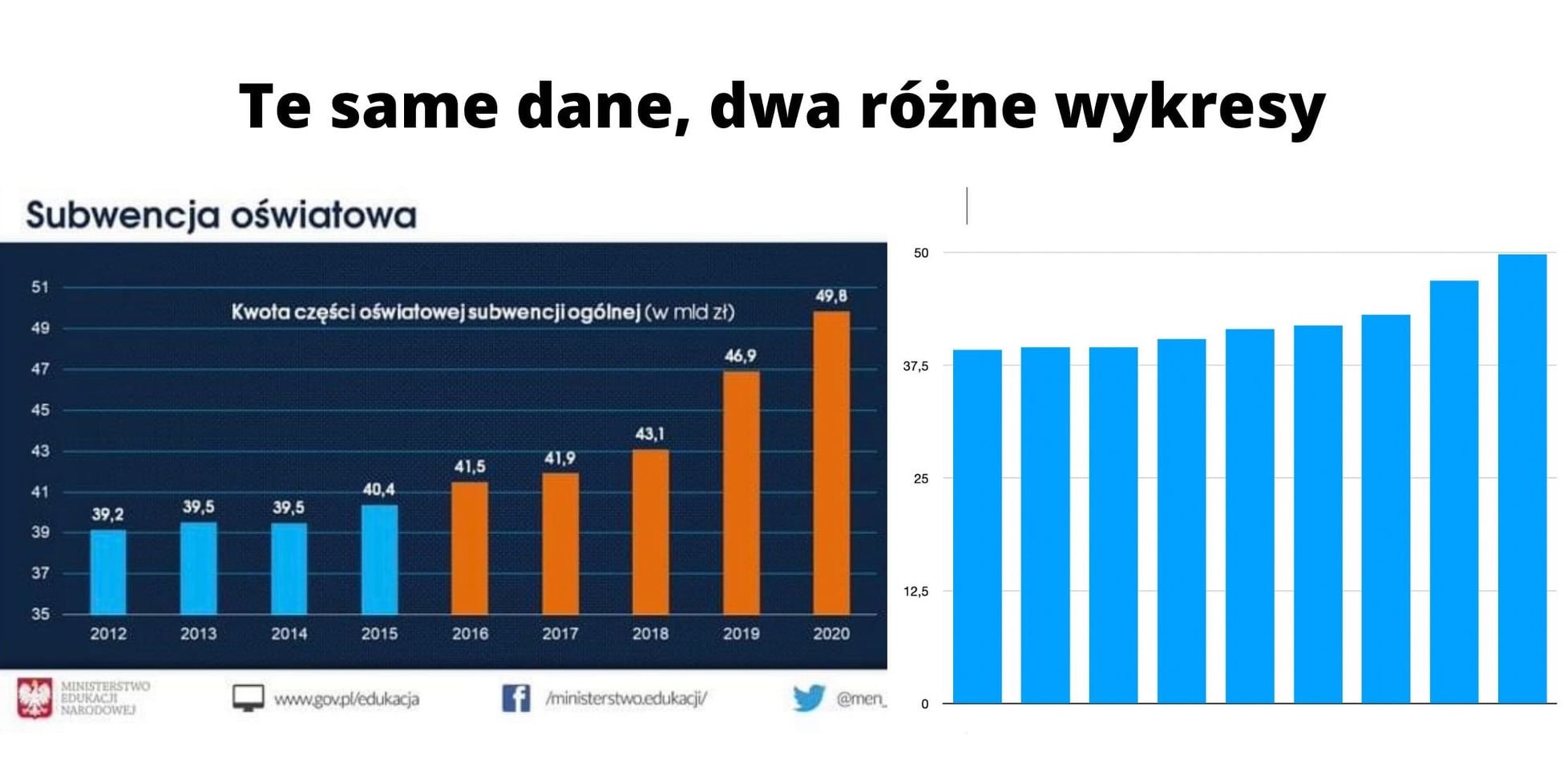
Warto zaprzyjaźnić się z królową nauk chociażby po to, by nie dawać się oszukać wykresom, których skala y sprytnie nie zaczyna się od 0

W każdym razie w tym badaniu wzięło udział 837 par bliźniaków jednojajowych (to takie, które mają identyczny materiał genetyczny) i 1422 par bliźniaków dwujajowych (mają różny materiał genetyczny, choć często wspólne zabawki). W badaniu tym mierzono odziedziczalność (ang. heritability) zmysłu matematycznego. Którą to odziedziczalność definiujemy jako proporcja wariancji w jakiejś funkcji, która może zostać wyjaśniona poprzez wariancje w DNA. Ważne! Jest to statystyka opisowa, czyli specyficzna dla konkretnego wieku i populacji (w tym wypadku – szesnastolatków z Wielkiej Brytanii), nie da się jej wygeneralizować. To znaczy, że możemy się tej wartości z zainteresowaniem przyjrzeć, niemniej w tym wypadku wnioski to naprawdę nie paprotki, żebyśmy je sobie tak przesadzali z miejsca na miejsce. 

Oto nadszedł ten moment  – czas by zaprosić na scenę naszą gwiazdę, poproszę o werble.

Okazało się mianowicie, że w tym badaniu odziedziczalność zmysłu matematycznego wyniosła… 32%. I nie było żadnych różnic między płciami! No i proszę bardzo, wszyscy klaszczą, słonie kłaniają się przy wodopoju, godność kapusty przywrócona! 

Bo to wszystko – te liczące niedźwiedzie, niemowlaki, bliźniaki, to w gruncie rzeczy dobre wiadomości. Bo to oznacza – że tak pozwolę sobie zacytować swoją własną książkę, co to ja ją napisałam, a Ty KUP JĄ!!!, że:

„Myślę, że to, co jest najtrudniejsze w uczeniu się statystyki, to głębokie przekonanie wielu ludzi, że kompletnie się do tego nie nadają. Najczęściej dlatego, że ktoś im kiedyś powiedział, że nie dadzą rady, że się tego nigdy nie nauczą, że to nie dla nich. Lubię powtarzać, że nie ma głąbów matematycznych, są tylko źli nauczyciele. Że każdy może się nauczyć poprawnego wnioskowania i mentalnie poprzytulać się z dowolnym modelem regresji. Jeśli w jakiejś szufladce w głowie trzymacie kartkę, na której ktoś kiedyś napisał Wam: „humanistyczny umysł”, „głąb matematyczny”, „liczbowy analfabeta”, to jest to najlepszy moment, by ją zgnieść i rzucić na pożarcie kotom. Kto nie ma kota w domu, może ją wyrzucić do śmieci. Byle do segregowanych”.

– „Statystycznie rzecz biorąc. Czyli ile trzeba zjeść czekolady, żeby dostać Nobla”, strona 14

Ewentualnie możecie tę absurdalną kartkę rzucić jakiejś mątwie. Chyba, że ta akurat będzie zajęta dzieleniem ziemniaków przy obiedzie, żeby nie było, że mątwa Tomasz dostanie ich więcej i później ziemniaczki zostawi, a krewetki zje. 

Wersja papierowa i e-book: [KLIKU KLIKU]

Audiobook: [KLIKU KLIKU]

Bibliografia

Brannon, E. M. (2005). What animals know about numbers. Handbook of mathematical cognition, 85-107.

Dehaene, S. (2011). The number sense: How the mind creates mathematics. OUP USA.

McIntosh, A., Reys, B. J., & Reys, R. E. (1992). A proposed framework for examining basic number sense. For the learning of mathematics, 12(3), 2-44.

Rumbaugh, D. M., Savage-Rumbaugh, S., & Hegel, M. T. (1987). Summation in the chimpanzee (Pan troglodytes). Journal of Experimental Psychology: Animal Behavior Processes, 13(2), 107.

Starr, A., Libertus, M. E., & Brannon, E. M. (2013). Number sense in infancy predicts mathematical abilities in childhood. Proceedings of the National Academy of Sciences, 110(45), 18116-18120.

Tosto, M. G. et al. (2014). Why do we differ in number sense? Evidence from a genetically sensitive investigation. Intelligence, 43, 35-46.

Xu, F., Spelke, E. S., & Goddard, S. (2005). Number sense in human infants. Developmental science, 8(1), 88-101.